SERVICE PROTOTYPE

• the high frequency fluctuations of the phase signals (with a focus on the L2-L1, the geometry free linear combination),
• the ratio of L2 signal losses and cycle slips,
• the signal-to-noise-count fluctuations.

From the first indicator, an empirical scintillation index is calculated along each satellite-receiver link over time intervals of 5 mn for 30 s samples and 1mn for 1 s samples. This index is then plotted at the sub-ionospheric point i.e. where the signal crosses the maximum density ionospheric layer considered at the fixed altitude of 400 km. The scintillation index is scaled to show the following levels of perturbations:

• low in the range of [0-0.25],
• medium in the range of [0.25-0.5],
• strong in the range of [0.5-0.75],
• severe when higher than 0.75.

The second indicator "L2 losses" is plotted as complementary information considering that the L2 signals frequently drop out during ionospheric scintillations. This behaviour has been observed whatever the geodetic receiver type. The third indicator is, at the present status of the investigation, difficult to calibrate. The explanation is that the required transformation from the signal-to-noise-count parameter into the C/No (carrier-to-noise-power-density ratio) parameter can’t be processed systematically. It is due for part of the receivers to a loss of parameter record accuracy or, in some cases, to a lack of manufacturer ancillary information.

What are the indicators mapped?

The first indicator is the high frequency GPS phase fluctuations on "L2-L1", the geometry free linear combination.
The "L2-L1 rate of change" - L2 and L1 being the phase observations on both GPS frequencies transformed in meters - may be an effective indicator of the GPS sensitivity to the ionospheric activity. The simple combination of the carrier phase observations (L2-L1) also called the geometry free is applied in order to eliminate the geometry: the distance to the satellite, the tropospheric propagation, the clock errors. Only remains the ionospheric correction and the phase ambiguities of L1 and L2 data. To identify the ionospheric scintillation occurrence, one has to apply a high pass filtering. A specific process separates most of the multipaths effects. A standard deviation is calculated over 5 minutes for the 30 s repetition rate or over 1 minute for the 1 s repetition rate along each satellite pass with the condition that no cycle slip happens during the interval. An empirical normalisation is done based on the level of noise calculated statistically for each type of receiver in quiet or stormy geomagnetic conditions and using the scintillation monitor at Douala (Cameroun).

One takes notice that the GPS perturbations are monitored only inside the coverage of the receiver network. For each "L2-L1 rate of change" global hourly map, this coverage can be easily deduced as each receiver-satellite link leads to a dot (one per 1mn or 5 mn interval). Another point is that some perturbations with similar signature mainly the multipaths may have not been completely filtered. They are still under investigation.

The second indicator is the ratio of L2 signal losses.
The "L2 losses" is an indicator for the losses of lock of the GPS satellite L2 signal tracking. Cycle slips on L2 are also considered as losses. To minimize the count of L2 dropouts of other origin than the ionosphere (multipaths, low signal-to-noise ratio...) observations under 15° degrees over the horizon are removed. For each satellite pass, a ratio of L2 losses is calculated every 5 minutes for the 30 s repetition rate receivers (every minute for those with a 1 s repetition rate). To distinguish the possible correlations with the scintillations, a test is applied to the remaining L2 signals that should correspond to a (L2-L1) term that goes over a threshold. The indicator is mapped only when greater than 10%.

Comparison with ionospheric monitors

With ionospheric scintillation monitors (Douala 2004, Ascension 2000, Alaska 1998).

Permanent calibration

A Ionospheric Scinitllation monitor (ISM) will be installed at Kourou (French Guyana) at the end of 2004. Kourou is a relevant site for monitoring the scintillations. It is located near the geomagnetic equator and two GPS permanent receivers are operating at both 30 s and 1 s repetition rate

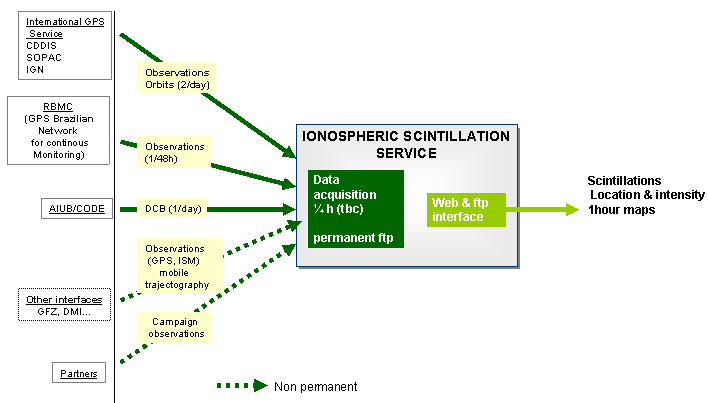
IONOSPHERIC SCINTILLATION SERVICE

Copyright © 2003-2005